3728. Cut a graph
The undirected
graph is given. Two types of operations are performed on graph in the given
order:
·
cut – cut a
graph, or delete an edge from a graph;
·
ask – check, whether
two given vertices lie in the same connected component.
It is known that
after performing all types of cut operations there is no edges
left in the graph. Give the result for each ask operation.
Input. The first line contains three integers – the number
of vertices n in a graph, the number of edges m and
the number of operations k (1 ≤ n ≤ 50000, 0 ≤ m
≤ 105, m ≤ k ≤
150000).
The next m lines define the graph edges; i-th
line contains two integers ui and vi (1 ≤ ui, vi ≤ n) – the end
numbers of the i-th edge. The
vertices are numbered starting from one; graph does not contain multiple edges
and loops.
The next k lines describe the operations.
Operation of type cut is given with the line “cut u v” (1 ≤ u, v ≤ n), which means that the edge
between the vertices u and v is deleted from a graph. Operation of
type ask is given with the line “ask u v” (1 ≤ u, v ≤ n), which means that you need
to know are the vertices u and v in the same connected component. It is
guaranteed that each edge of the graph meets in cut operations exactly
once.
Output. For each ask
operation print in a separate line the word “YES”, if two given vertices are in
the same connected component, and “NO” otherwise. The order of answers must
match the order of ask operations in input data.
|
Sample
input |
Sample
output |
|
3 3 7 1 2 2 3 3 1 ask 3 3 cut 1 2 ask 1 2 cut 1 3 ask 2 1 cut 2 3 ask 3 1 |
YES YES NO NO |
SOLUTION
disjoint sets
Algorithm analysis
Save all requests and start processing them
in the reverse order. Start with a graph that does not contain edges (after all
cut
operations are performed, the set of edges is empty). To process the request “cut u v”, we will add an edge between
the vertices u and v. When the request “ask u v” arrives, we will check whether
the vertices u and v lie in the same connected component. Store
the answers to ask requests in the reverse order. Then print them in the
required order.
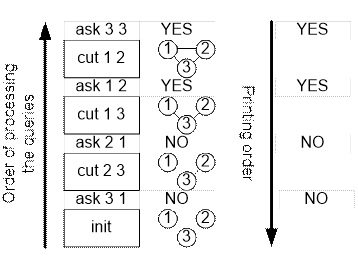
Example
Consider the
order of processing the requests for the sample given and the order of printing
the responses to the queries.
Algorithm
realization
Save the operations
in the mas array: mas[0][i] contains
0 if the i-th operation is cut and 1 if the
i-th operation is ask. mas[1][i] and mas[2][i] contain the corresponding u and v query values.
The dsu array is used to process a disjoint set. res is an array of resulting responses.
#define MAX 150010
char op[20];
int mas[3][MAX], dsu[MAX], res[MAX];
Function Repr
returns the representative of the set that vertex n belongs to.
int Repr(int n)
{
if (n == dsu[n]) return
n;
return dsu[n] = Repr(dsu[n]);
}
Function Union unites the sets to
which the vertices x and y belong.
int Union(int x, int y)
{
int x1 = Repr(x),y1 = Repr(y);
dsu[x1] = y1;
return (x1 == y1);
}
The main part of
the program. Read the values n, m,
k. The initial state of the graph can
be skipped.
scanf("%d %d %d",&n,&m,&k);
for(i = 0; i < m; i++) scanf("%d %d",&u,&v);
scanf("\n");
Store the input queries in the mas array.
for(i = 0; i < k; i++)
{
scanf("%s %d %d\n",op,&mas[1][i],&mas[2][i]);
if (op[0] == 'a')
mas[0][i] = 1; else mas[0][i] = 0;
}
Initialize the dsu array (vertex i points to
itself).
for(i = 1; i <= n; i++) dsu[i] = i;
Process the
queries from the
end
to the start. If the i-th query is ask (mas[0][i] is equal to 1), then we set res[i] to one, provided that the vertices u and v are in the same connected component (and we set res[i] = 0 otherwise ).
for(i = k - 1; i >= 0; i--)
{
if (mas[0][i]) res[i] = (Repr(mas[1][i])
== Repr(mas[2][i]));
else Union(mas[1][i],mas[2][i]);
}
Print the answers to sequentially incoming queries. If the i-th query is ask,
then we print the answer
depending on the value of res[i].
for(i = 0; i < k; i++)
if (mas[0][i])
if (res[i]) printf("YES\n"); else
printf("NO\n");